Physics
During my PhD at College de France (2020-2023), I developed 3D image analysis algorithms for biology based on physical principles.
Embryo Mechanics Cartography

I’ve developed a pipeline to create 3D tension maps of forces in tissues. The idea is the following one: if we have an accurate view of the geometry of cells, and a physical model of the mechanics of these cells, we can infer the forces at play in an embryo simply by looking at its shape. Membranes that are tensed will tend to be flat. Membrane that are relaxed will tend to be curved. The difficulty is then to characterise the geometry of whole embryos. Confocal microscopes offers awesome snapshots of these biological objects. But extracting the geometry of these 3D images is not trivial.
I combined 3D deep neural networks and tools from discrete differential geometry to accurately measure curvatures on discrete surfaces. We applied this algorithms on ascidians, worm and mouse embryos to characterise the forces at play during their development.
This work got highlighted by the CNRS, the Company of Biologists and Nature Methods !
Inference of membrane flows using optimal transport
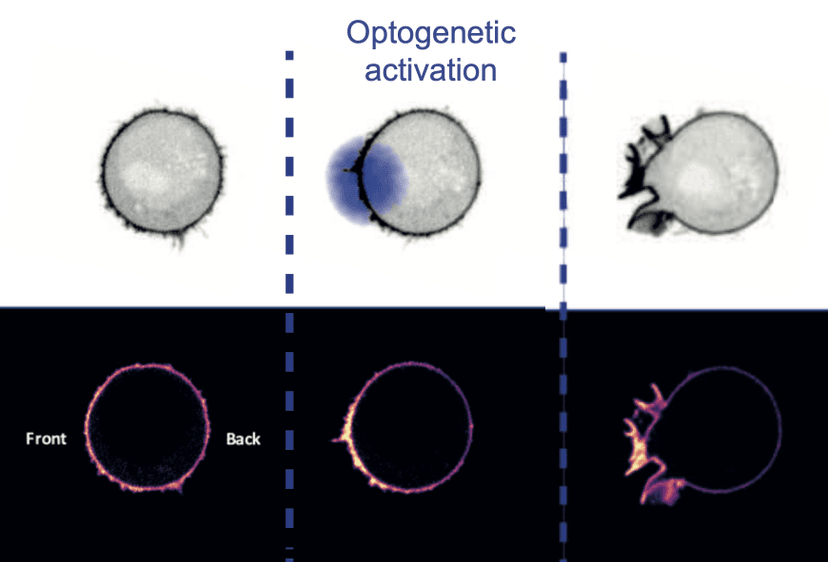
This project was done in collaboration with researchers from UCSF and Berkeley. We wanted to understand how cells membranes generated and transmited tensions. On the experiments, we observed membrane flows, but had no way to quantify these flows.
I developed a novel method to analyze and quantify membrane flows from microscopy movies using optimal transport. I started from kymographs, a graphical representation of spatiotemporal concentration of membrane markers, and find the most plausible velocity field by inverting evolution equations describing the evolution of the concentration of membrane markers.
The methodology used -starting from microscopic equations, and coarse-graining them to derive a master equation- is widely used in statistical physics to describe the evolution of complex systems. It was very satisfying to apply these tools to solve real problems in biology.
Differentiable Rendering for fluorescence microscopy
Ichbiah, S., Delbary, F., Turlier, H. Differentiable Rendering for 3D Fluorescence Microscopy

We developed an algorithm to generate artificial 3D microscopy images from simulations. Artificial images are very important in years to come, as they will be used to generate training data for deep learning algorithms. We reproduced the functioning of a confocal microscope, where a surface is scanned by a laser, and the emitted fluorescence is captured by a camera.
The interesting feature of this algorithm is that it is differentiable. We can compute all the gradients to optimize the parameters of the microscope, or the surface, to fit the data. This gives as a physically-principled algorithm to retrieve shapes of embryos from microscopy data.
Mathematically, we need, for each voxel, to compute the convolution of the surface with the point spread function of the microscope. 3D microscopy images are HUGE. To make the computation tractable, I had to use a lot of tricks, and of course, parallized the computation on GPUs by writing CUDA kernels for the forward and the backward pass.
There is a kind of magic when you derive equations, discretize and implement them, and then see that it just works ! This work is not yet published, but i am very excited by all the applications it would unlock for microscopy image analysis.